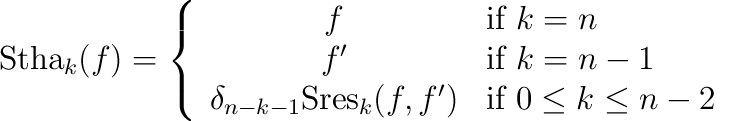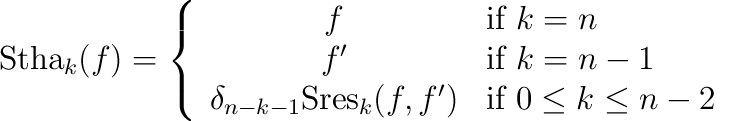\begin{ccRefConcept}{PolynomialTraits_d::SturmHabichtSequence}

\textbf{Note:} This functor is optional!

\ccDefinition

Computes the Sturm-Habicht sequence 
(aka the signed subresultant sequence)
of a polynomial $f$ of type 
\ccc{PolynomialTraits_d::Polynomial_d} with respect to a certain variable $x_i$.
The Sturm-Habicht sequence is similar to the polynomial subresultant sequence
of $f$ and its derivative $f':=\frac{\partial f}{\partial x_i}$
with respect to $x_i$. The implementation is based on the following definition:

Let $n:=\deg f$ and $\delta_k:=(-1)^{k(k+1)/2}$. 
For $k\in\{0,\ldots,n\}$, the {\it $k$-th Sturm-Habicht polynomial} 
of $f$ is defined as:

\begin{ccTexOnly}
$$\mathrm{Stha}_k(f)=\left\{\begin{array}{cl}
f & \textrm{if\ } k=n\\
f' & \textrm{if\ } k=n-1\\
\delta_{n-k-1}\mathrm{Sres}_k(f,f') &\textrm{if\ } 0\leq k\leq n-2
\end{array}\color{white}\right\}\color{black}$$
\end{ccTexOnly}

\begin{ccHtmlOnly}
<CENTER>
<IMG BORDER=0 SRC="./sturm_habicht_def.gif" ALIGN=middle ALT="Sturm-Habicht sequence">
</CENTER>
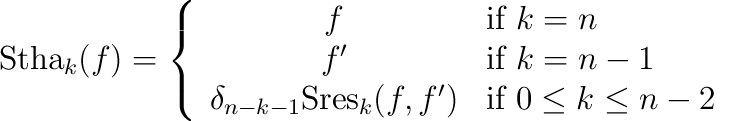\end{ccHtmlOnly}

where $\mathrm{Sres}_k(f,f')$ is defined 
as in the concept \ccc{PolynomialTraits_d::PolynomialSubresultants}.

The result is written in an output range, 
starting with the $0$-th Sturm-Habicht polynomial (which is equal to
the discriminant of $f$ up to a multiple of the leading coefficient).

\ccRefines 
\ccc{AdaptableBinaryFunction}\\
\ccc{CopyConstructible}\\
\ccc{DefaultConstructible}\\


\ccCreationVariable{fo}
\ccOperations
\ccMethod{template<typename OutputIterator>
        OutputIterator operator()(Polynomial_d   f,
                                  OutputIterator out);}
         { computes the Sturm-Habicht sequence of $f$, 
           with respect to the outermost variable. Each element is of type
           \ccc{PolynomialTraits_d::Polynomial_d}.}

\ccMethod{template<typename OutputIterator>
        OutputIterator operator()(Polynomial_d   f,
                                  OutputIterator out,
                                  int i);}
         { computes the Sturm-Habicht sequence of $f$ 
           with respect to the variable $x_i$.}

%\ccHasModels

\ccSeeAlso

\ccRefIdfierPage{Polynomial_d}\\
\ccRefIdfierPage{PolynomialTraits_d}\\
\ccRefIdfierPage{PolynomialTraits_d::Resultant}\\
\ccRefIdfierPage{PolynomialTraits_d::PrincipalSturmHabichtSequence}\\
\ccRefIdfierPage{PolynomialTraits_d::SturmHabichtSequenceWithCofactors}\\
\ccRefIdfierPage{PolynomialTraits_d::PolynomialSubresultants}\\

\end{ccRefConcept}